I received this reply from support about my issue:
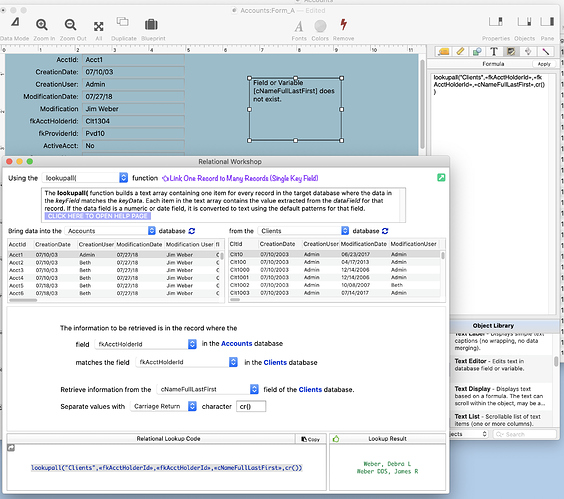
My question: I’ve used the Relational Workshop to create the code and see the correct result. I just haven’t got to how that is put into a record’s form to be able to view it there.
Support response: I think the answer you are looking for is that you take the formula generated by the Relational Workshop and put it into a Text Display Object. Text Display Object
The Relational Workshop gave the correct output but when I put into a Text Display Object and received a field not found error. See screenshot. All the fields appear on the form because I thought it might fix the problem if I had the reference field on the form, but that did not help.